Discrete Element Method

Intro

The Discrete Element Method (or Distinct Element Method) is a powerful method to describe the behaviour of granular materials starting from a micromechanical standpoint. Plasticity, large and localized strains, detachments and other important features of the behaviour of granular materials spontaneously arise from the nature of this method. In comparison to the Finite Element Method, DEM appears more physically based and it doesn’t require particular artificial mathematical conjectures.

Basics

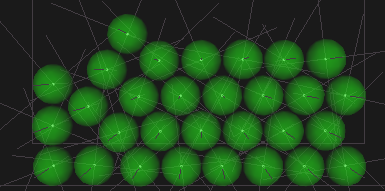
Each particle is independent, represented by its density, shape, position in the space and mechanical behaviour at the contact. As first approximation particles are treated as undeformable. Overlaps between particles produce normal repulsive forces (linear or non-linear, elastic or plastic) and tangential frictional forces. Long-range attractive forces can be also taken into account for modelling cohesive materials and capillary bridges. All these forces are added to the gravitational ones. The position of each particle is updated at each time-step by integrating Newton’s equation of motion with a certain explicit time integration scheme and considering relative translation and rotation.

The time-step must be chosen small enough to avoid discretization errors and to ensure the energy conservation and then the reliability of the numerical simulation.

The simplest 3D shape for a DEM algorithm is the sphere for which the contact detection algorithm reduces to a simple inequality check. Other shapes are possible but they may dramatically increase the computational cost of simulations and the complexity of the contact mechanics. Moreover, it must be noted that no accordance exists about contact mechanics with different shapes due to the complexity of the phenomena.

The most time-consuming factor is related to the number of contact checks that must be performed. Some tricks permit to decrease the number of checks generally dividing the space into smaller sub-spaces with a lower number of potential contact and temporary saving their particle populations.

The other issue regards the critical time-step which essentially depends on the mass of the smaller particle and the elastic stiffness at the contact. If the time-step results very small many steps (and then many calculations) could be required to simulate a short laboratory experiment.

Example of applications

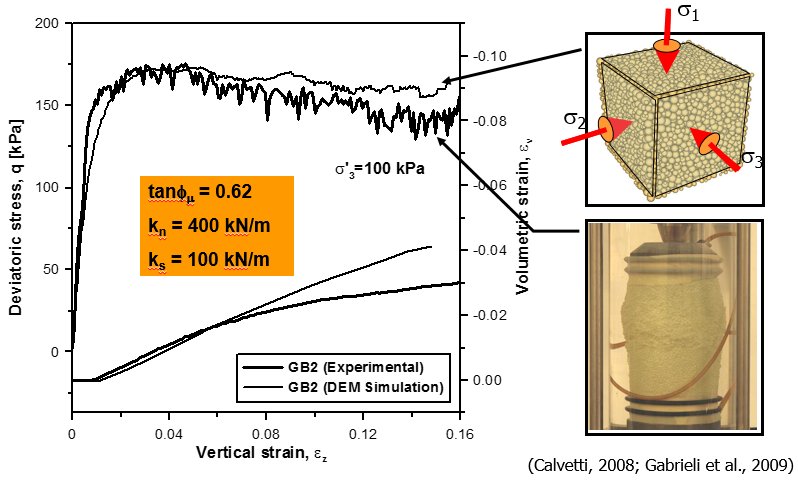
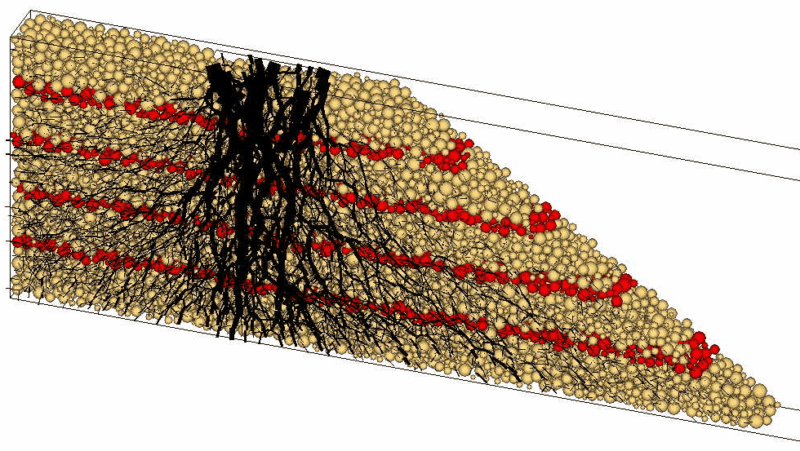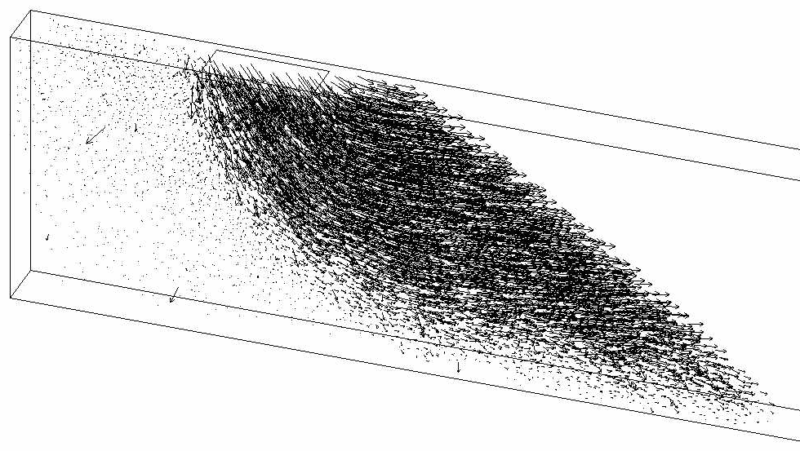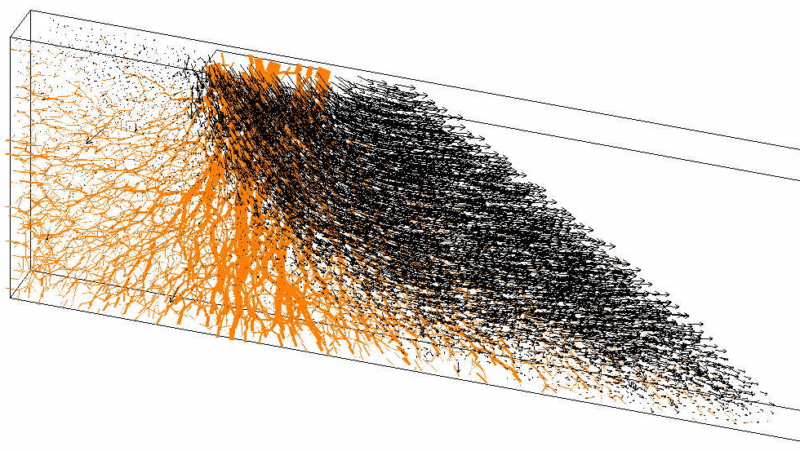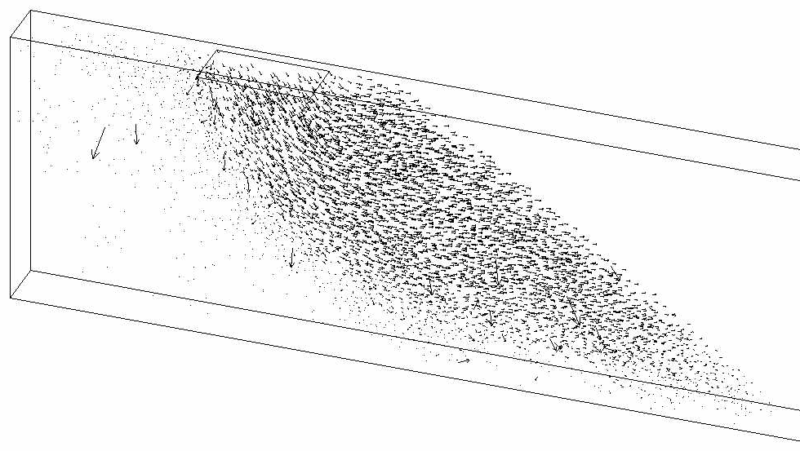
With DEM it is possible to describe granular materials in quasi-static problems (e.g. triaxial tests, simple shear tests, load on foundations,…) as well as dynamic problems (e.g. impacts, granular flows, collapses,…). Particular structures like wire meshes and geogrids can be also modelled with DEM. Some screenshots of these examples are reported here:

References