As the lengthscales of a system are decreased by some orders of magnitude the relative importance of physical laws drastically changes. It is the case of capillary forces in water which arises when the scale reaches the millimetre.
The capillary bridge or meniscus or liquid ring is a little amount of liquid that is stable between two particles or more generally between two surfaces.
Surface tension and properties of the liquid-solid interface enable liquid to get stuck on particles. Indeed, the effect of gravity is negligible if the
When two spherical particles share a capillary bridge they experience a normal attractive force $latex F_{cap}$ that is a
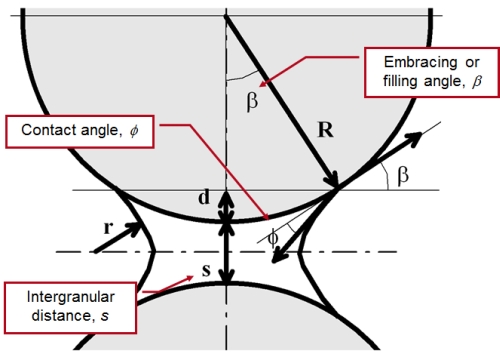
- the particle radius, $latex R$
- the capillary volume, $latex V$
- the distance (gap), $latex s$
- the liquid surface tension, $latex \gamma$
- the contact angle, $latex \phi$
Several methods can be used to compute the capillary force:
- numerical solution of the Young-Laplace equation (e.g. Lian et al, 1993)
- using empirical/approximated relationships starting from Young-Laplace equation (e.g. Soulié et al., 2006; Willet…)
- numerically solving the minimum energy problem (e.g. with Surface Evolver; Brakke, 1992)
- using approximate theoretical solution starting from the minimum energy approach (Israelachvili, 1992; Rabinovich et al., 2005; Lambert et al., 2008)
The latter leads to a simple analytical formula suitable for coupling with the Discrete Element Method
$latex F_{cap} = \frac{ 2 \pi R \gamma \cos \phi }{ 1+ \left[ s / 2 d \left ( s , V \right ) \right ] } $
with
$latex d \left ( s , V \right ) = \frac{ s }{ 2 } \left ( -1 + \sqrt{ 1 + \frac{ 2 V }{ \pi R s^2} } \right) $
All the geometrical variables are sketched in Figure 1.
In this case, the capillary attraction force must be eventually added to the classical repulsive force at the contact.
For higher water contents, in the funicular state, the capillary forces are between three or more particles .
The effect of the water content on a granular material was studied with reference to some collapse tests carried out in the laboratory and modelled with DEM.
Here are some results:
